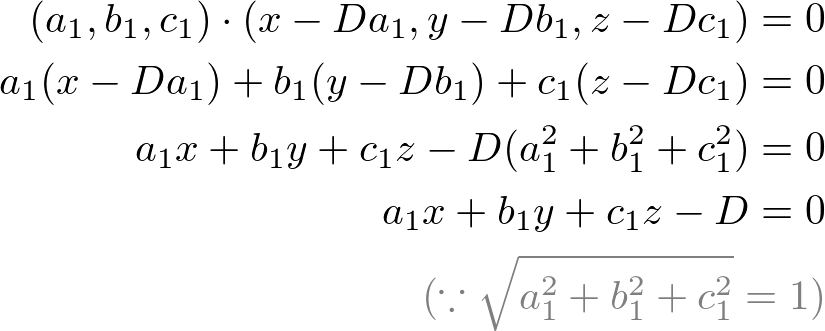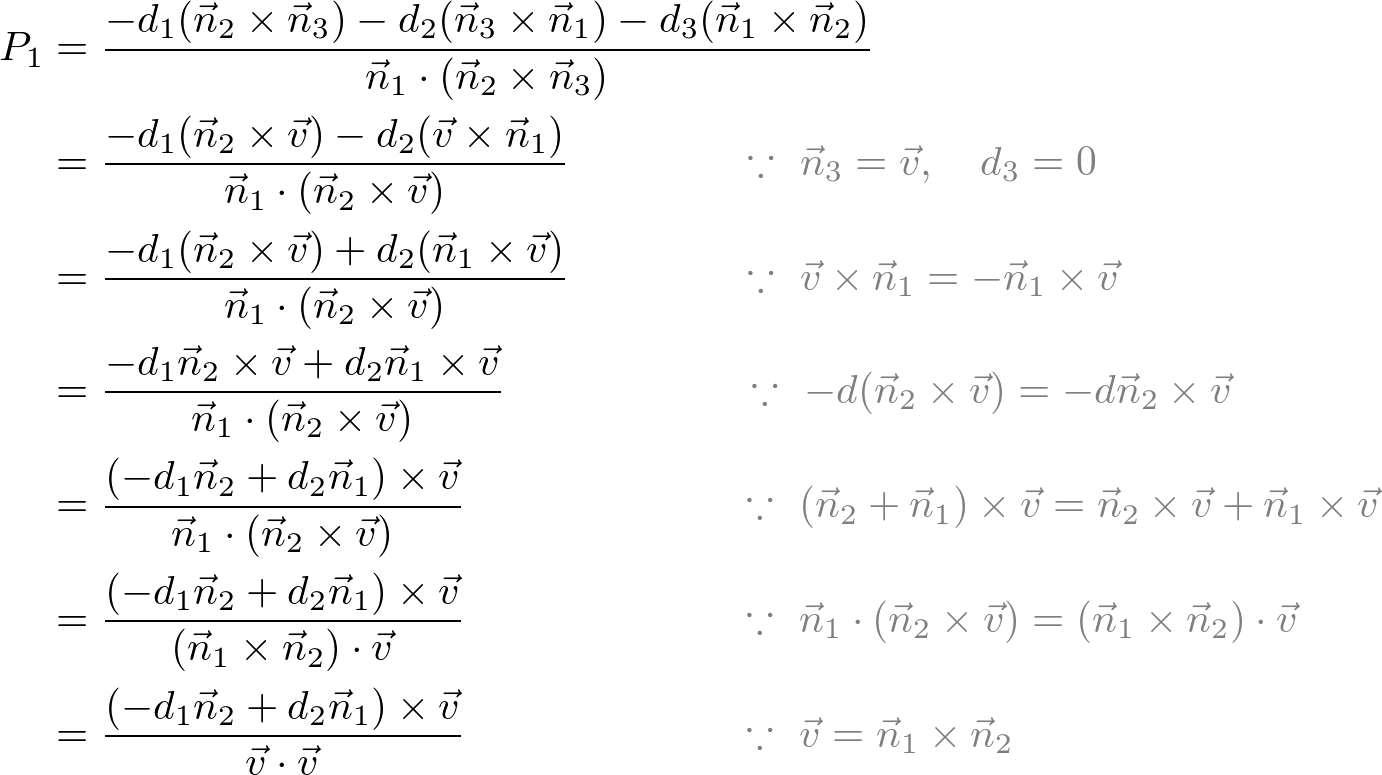Unit Vector Orthogonal To Two Vectors 3d
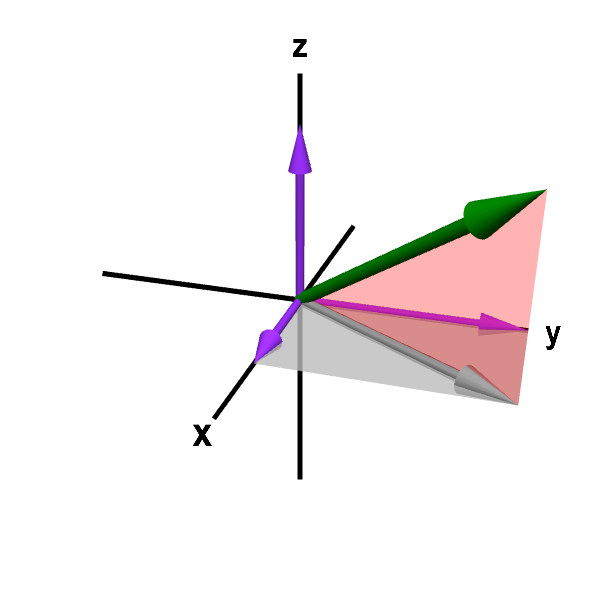
Orthogonal vectors in space exercises.
Unit vector orthogonal to two vectors 3d. Try to solve exercises with vectors 3d. When interpolating from one orthonormal matrix to another the intermediate ones will have orthogonal rows and columns but not unit length. The projections of vector a along the x y and z directions are a x a y and a z respectively. To construct a vector that is perpendicular to another given vector you can use techniques based on the dot product and cross product of vectors.
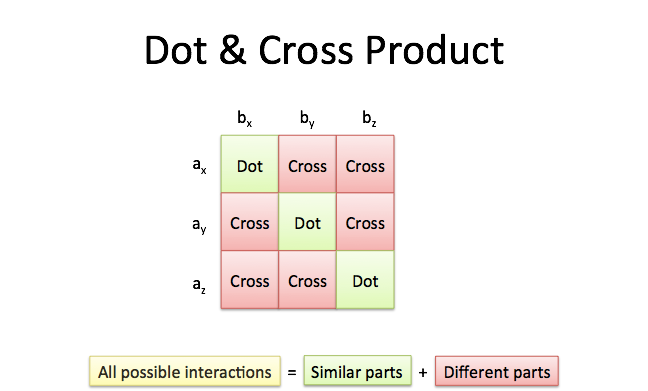
Most noteworthy in euclidean space the dot product of two unit vector is a scalar value amounting to the cosine of the smaller subtended angle. Addition and subtraction of two vectors in space exercises. A set of three mutually orthogonal unit vectors right handed system. We say that 2 vectors are orthogonal if they are perpendicular to each other.
If the rows and columns are orthogonal unit vectors it s an orthogonal matrix. Dot product of two vectors in space exercises. A b a1 b2 a2 b2 a3 b3. A vector of unit length.
Vectors a and b are orthogonal when n 2. Also in a 3 dimensional 3d euclidean space the cross product of two random unit vectors is a third vector orthogonal to both of them having a length equal to the sine of the smaller subtended angle. A coordinate system represented by base vectors which follow the right hand rule. Base vectors for a rectangular coordinate system.
Component form of a vector with initial point and terminal point in space exercises. The dot product of the two vectors is zero. If two vectors are perpendicular then their dot product is equal to zero.